画像をフーリエ変換して何をするかといえば、やっぱりフィルタですよね。
ということで今回は画像をフーリエ変換してローパスフィルタ、ハイパスフィルタを試してみたのでそれを記事にします。
今回使用する画像は以下の画像です。
Contents
ローパスフィルタ
まず初めに単純に高周波成分をカットして低周波成分だけを通過させるローパスフィルタを試してみました。
やり方は簡単で、フーリエ変換して位相シフトした画像と同じサイズの配列を作成し低周波成分にあたる部分を1、高周波成分にあたる部分を0とします。
その配列と、フーリエ変換後の配列を掛け算することでできます。
import numpy as np
import matplotlib.pyplot as plt
img = pydicom.dcmread('CT000034')
pix_arr = img.pixel_array # 変数pix_arrにピクセルデータを格納
fft_arr = np.fft.fft2(pix_arr) # 変数fft_arrにpix_arrをフーリエ変換したデータを格納
fft_arr_shift = np.fft.fftshift(fft_arr)
filter = np.zeros(fft_arr.shape)
center_x = fft_arr.shape[1]//2
center_y = fft_arr.shape[0]//2
filter[center_y-50: center_y+50 ,center_x-50: center_x+50 ] = 1
fft_arr_shift_filter = fft_arr_shift * filter
fft_filter = np.fft.fftshift(fft_arr_shift_filter) # 位相シフトを戻す
fft_filter = np.fft.ifft2(fft_filter) #逆フーリエ変換
fig = plt.figure()
ax1 = fig.add_subplot(2,3,1)
ax2 = fig.add_subplot(2,3,2)
ax3 = fig.add_subplot(2,3,3)
ax4 = fig.add_subplot(2,3,4)
ax5 = fig.add_subplot(2,3,4)
ax6 = fig.add_subplot(2,3,6)
ax1.imshow(np.abs(fft_arr_shift.real), cmap='gray', vmax =500000)
ax2.imshow(np.abs(filter), cmap='gray')
ax3.imshow(np.abs(fft_arr_shift_filter), cmap='gray', vmax =500000)
ax4.imshow(pix_arr, cmap='gray')
ax6.imshow(np.abs(fft_filter.real), cmap='gray')
plt.show()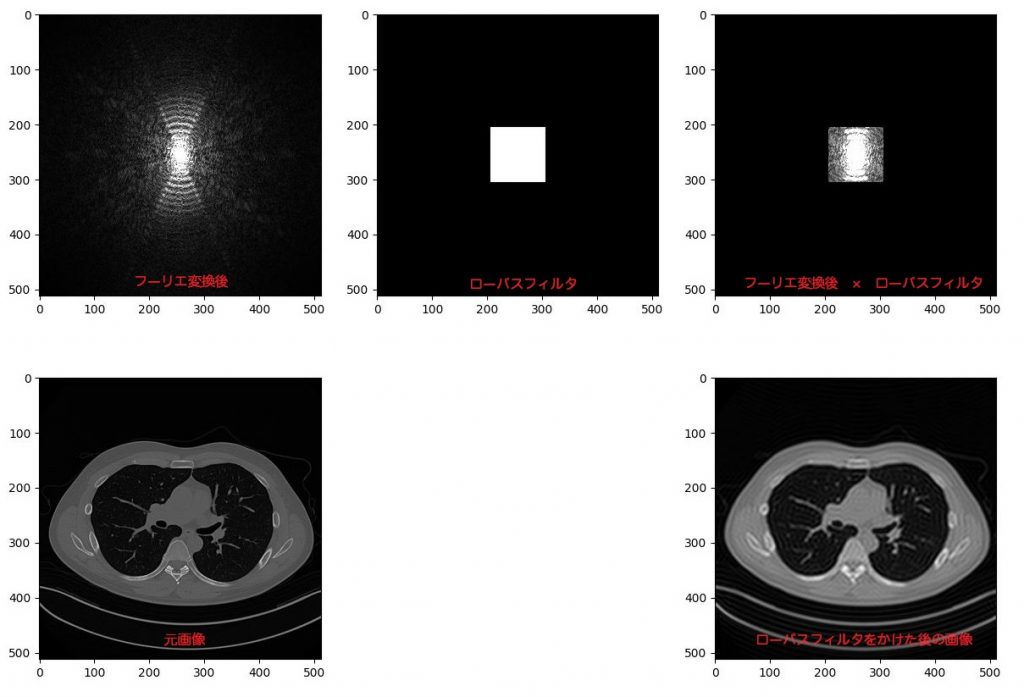
画像が小さくてわかりずらいかもしれませんが、画像のシャープさがなくなっているのが分かります。(クリックすると拡大します。)
フィルタの1の領域をもう少し小さくしてみます。上記コードの14行目を書き換えます。
filter[center_y-5: center_y+5 ,center_x-5: center_x+5 ] = 1
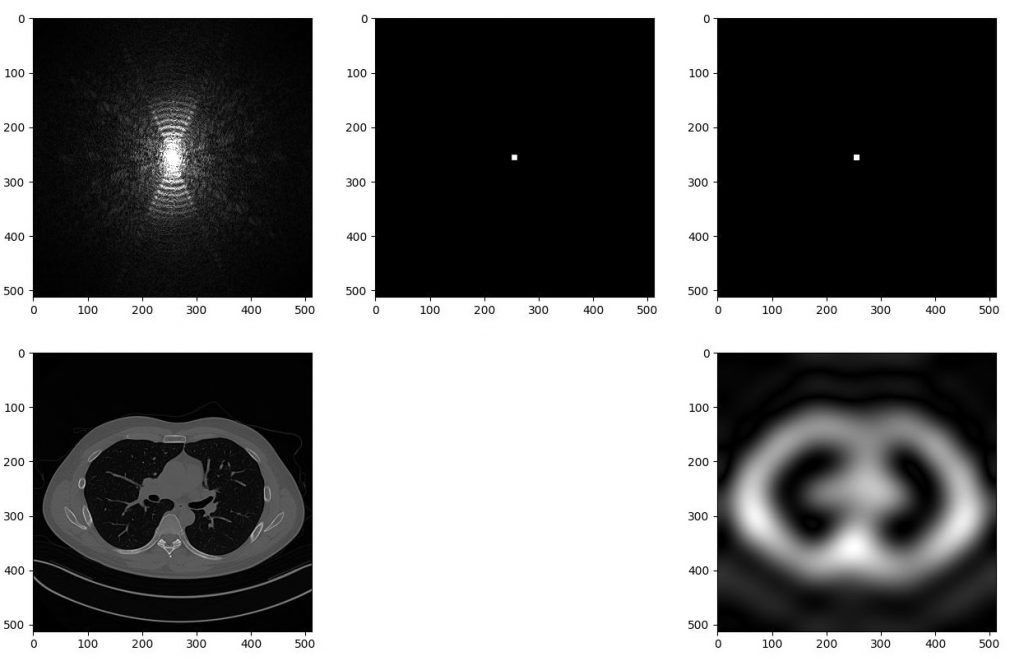
前のフィルタの1/10にしたらアイソトープのような分解能の画像になってしまいました。。。。。
ハイパスフィルタ
今度はハイパスフィルタをやってみます。
先ほどは、0で初期値設定した配列を作成しましたが、今度は1で初期化した配列を作成し、中心部を0で埋めた配列を作成してハイパスフィルタを作成します。
import numpy as np
import matplotlib.pyplot as plt
img = pydicom.dcmread('CT000033')
pix_arr = img.pixel_array # 変数pix_arrにピクセルデータを格納
fft_arr = np.fft.fft2(pix_arr) # 変数fft_arrにpix_arrをフーリエ変換したデータを格納
fft_arr_shift = np.fft.fftshift(fft_arr)
filter = np.ones(fft_arr.shape)
center_x = fft_arr.shape[1]//2
center_y = fft_arr.shape[0]//2
filter[center_y-100: center_y+100 ,center_x-100: center_x+100 ] = 0
fft_arr_shift_filter = fft_arr_shift * filter
fft_filter = np.fft.fftshift(fft_arr_shift_filter) # 位相シフトを戻す
fft_filter = np.fft.ifft2(fft_filter) #逆フーリエ変換
fig = plt.figure()
ax1 = fig.add_subplot(2,3,1)
ax2 = fig.add_subplot(2,3,2)
ax3 = fig.add_subplot(2,3,3)
ax4 = fig.add_subplot(2,3,4)
ax5 = fig.add_subplot(2,3,4)
ax6 = fig.add_subplot(2,3,6)
ax1.imshow(np.abs(fft_arr_shift.real), cmap='gray', vmax =500000)
ax2.imshow(np.abs(filter), cmap='gray')
ax3.imshow(np.abs(fft_arr_shift_filter), cmap='gray', vmax =500000)
ax4.imshow(pix_arr, cmap='gray')
ax6.imshow(np.abs(fft_filter.real), cmap='gray')
plt.show()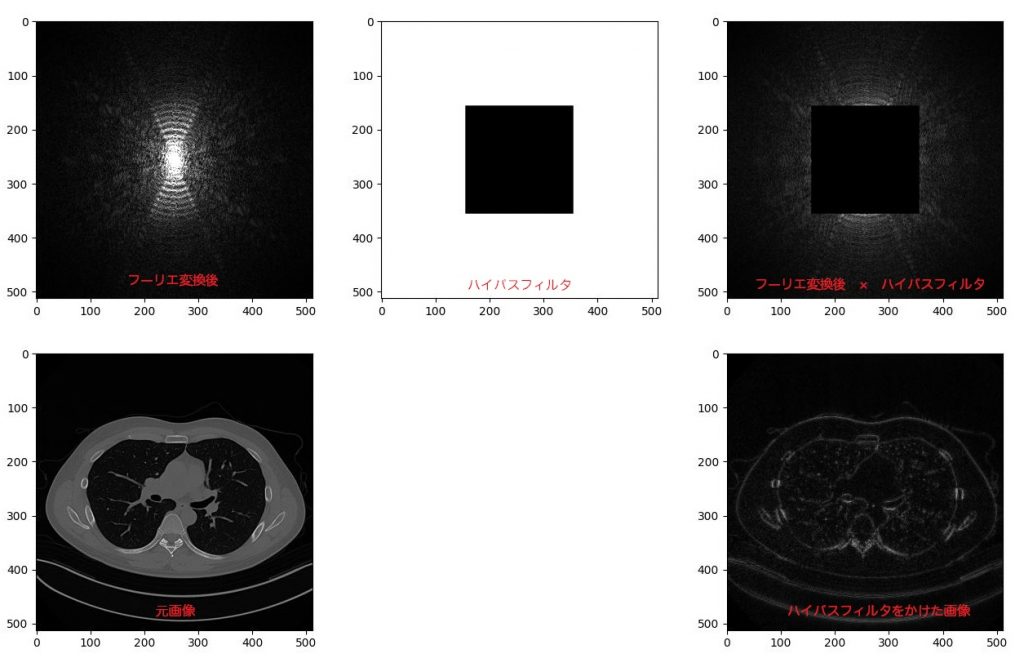
いかがでしょう!!今度は輪郭部分が強調された画像が作成されました。
最後に
原理は分かっていても、実際にコードを組んでやってみるとおもしろいですね。
今回は簡単なフィルタでしかも、フィルタが1というものしか試していませんが、1.5や2といったものを試してみても面白いかもしれませんね。
ぜひとも、試してみてください。
おつかれさまでした。
